An illustrated counterexample to the smooth four dimensional Poincare conjecture

Well, at least that’s what DALL·E 2 showed me. (Wiki)

A sketchy surgery description of the Seifert-Weber Dodecahedral space

Gates Rudd, Dunfield, and Obeidin just put out their preprint Computing a link diagram from its exterior. It describes “the first practical algorithm for finding a diagram of a knot given a triangulation of its exterior”. Neat. Really neat. I’ve been doing it the hard way.

As one application of their work, they found a surgery diagram of the Seifert-Weber Dodecahedral space. Here’s Figure 21 of Section 9.2.

Surgery description of the Seifert Weber space by Gates Rudd, Dunfield, and Obeidin

Here’s one I came up with back in September 2019 in response to a MathOverflow question but never got around to cleaning up for public consumption.

A sketchy surgery description of the Seifert Weber space

Below we’ll take a look at some of the sketches that led to this surgery description.

Reflections

Oh, here I am.

That’s an image I created for the upcoming ICERM workshop Perspectives on Dehn surgery. Go ahead, click that link.

This workshop is partially supported by Josh Greene’s NSF CAREER award, so please ask for the funding you’d require to be able to attend. Please disregard the standard language on the ICERM application page concerning limited graduate student funding. In particular, you do not need to prepare a poster to be eligible for funding.

As you may have noticed, something is awry with the reflection. Josh Greene gave the idea for this image when we were discussing posters for the workshop.

In contrast to most of the other images on the site, this was done with mostly Illustrator and some Photoshop. However I did some test runs in Rhino regarding refractions, reflections, and ripples.

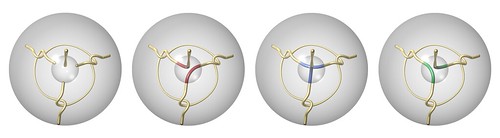
Reflective bandings

Let’s riff again on that Berge tangle.  The three-fold symmetry of the tangle in about one arc allows the three fillings to be equivalent.

If we double the tangle with the red filling (that is, glue it to its reflection across the outer sphere) we obtain the two component unlink.

 

Getting the unlink from doubling is due to these filled tangles being rational tangles, but nevermind that for now. Instead, ponder this curiosity. Let’s keep the mirrored red filling up top and compare the blue and green down below.

They’re the same except the small change between the blue and green filling.  (Taken together, the blue and green arcs bound a twisted rectangle, a “band”).  But they’re even closer in another way.  Mirror, then rotate:

 
Mirror the blue guy across the horizontal plane, then rotate about the central vertical axis by a third.  And now it’s the same as the green guy.

This generalizes quite nicely.

Mathematics with 3D Printing

Back in September I participated in a local Pecha Kucha event on the topic of 3D printing.  Of course I talked about interactions of mathematics and 3D printing.   The video (well, slides+audio) is now online.

I’d brought along some of the models of mine and others that I’d printed.  As you may pick up from the audio, I was tossing them out into the audience.  It was all fun and games until someone lost an eye. (The one from that last post has pointy corners.)

My sincerest apologies if I either misrepresented, misattributed, or didn’t mention someone’s work.  I don’t have complete knowledge of this blooming field and surely got some things wrong and overlooked some other things.   So by all means, please contribute corrections, updates, or further information in the comments.

Joining two segments

My how time flies…

The join of two topological spaces and is basically the space of all line segments between every pair of points.  As a nice embedded, visceral example of this, a tetrahedron may be viewed as the join of two skew line segments.

Indeed this is the illustration on Wikipedia.

It also arises naturally when you think about grid diagrams of knots.  Remember this from way back?

Thinking along those lines, you might consider discretizing it a bit…  Instead of taking the join of two entire segments, just take the join of points along each segment.

Here I’ve used .   And that gives us the complete bipartite graph naturally embedded as a subset of the tetrahedron.  Moreover, any grid number knot is a cycle in this particular embedding of the graph.

A Generalized Banding

The preprint Band Surgeries and Crossing Changes between Fibered Links by Buck-Ishihara-Rathbun-Shimokawa caught my eye this morning. They describe a describe a generalization of the plumbing of a Hopf band. Like Hopf plumbing, this operation preserves fiberedness. But unlike Hopf plumbing which occurs in a neighborhood of a disk, it is non-local occurring in a neighborhood of an annulus.

I thought I’d show the product disk associated to the band. This lets one verify the persistence of fiberedness and work out the resulting monodromy (which I haven’t done myself yet).

Twisting with Surgery

Here’s a sequence of images I drew for a talk I gave about a month ago. I reckon there isn’t much more to say that’s not in the images. Hit flickr for larger versions.

It’s full of surfaces!

That’s the exterior of the trefoil.   No, really.  I mean, well, it’s a torus embedded as the boundary of the exterior of a trefoil.

Okay, so it’s not how you’d probably choose to draw it.  It’s not how I’d first choose to draw it either.  Let’s see how I came to it.

Think about the space around the trefoil.  The thing’s hollow — it goes on (round and round) forever — and — oh my God

— it’s full of surfaces!   (That was terrible. My sincere apologies to Clarke.)

Chains and Tangles

These two links have homeomorphic exteriors.

They’re both strongly invertible. Let’s quotient the first link by its strong inversion to get a tangle. Then we’ll isotop that tangle around and eventually take its double branched cover to get the second.

Notice that this homeomorphism swaps the red and blue meridians and longitudes.